This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Yici Zhong, Department of Physics, Graduate School of Science, University of Tokyo, Bunkyo-ku, Tokyo 113-0033, Japan;
(2) Kazumi Kashiyama, Research Center for the Early Universe, Graduate School of Science, University of Tokyo, Bunkyo-ku, Tokyo 113-0033, Japan and Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU,WPI), The University of Tokyo, Chiba 277-8582, Japan;
(3) Shinsuke Takasao, Department of Earth and Space Science, Graduate School of Science, Osaka University, Toyonaka, Osaka 560-0043, Japan;
(4) Toshikazu Shigeyama, Research Center for the Early Universe (RESCEU), School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan and Department of Astronomy, School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan;
(5) Kotaro Fujisawa, Research Center for the Early Universe (RESCEU), School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-0033, Japan and Department of Liberal Arts, Tokyo University of Technology, Ota-ku, Tokyo 144-0051, Japan.
Table of Links
Appendix
C. Change of the Mass Loss Rate in MHD Regime
2. SETUP
We conduct a series of numerical simulations of a rotating magnetic wind from a massive WD merger product with a stable nuclear burning occurring at the near surface region. We first describe the general numerical setup including the governing equations, the Riemann solver, the mesh decomposition, and the boundary conditions in Sec. 2.1. We then describe the source term that represents the injection of mass and internal energy at the near surface nuclear burning region in Sec. 2.2. Finally, we elaborate on setups related to magnetic fields.
2.1. Magnetohydrodynamic (MHD) equations
We numerically integrate ideal MHD equations with central gravity;


We use the HLLD approximate Riemann solver for the MHD equations (Miyoshi & Kusano 2005) with the secondorder piecewise linear reconstruction method (PLM). The time integration is carried out by the second-order RungeKutta method with Courant-Friedrich-Lewy number of 0.1. The computational domain is resolved with the mesh number of 128 for [0.9, 30] R∗ in the radial direction and 128 for [0, π] in the polar direction. We employ a non-uniform mesh in the radial direction, where the radial grid size is proportional to the radius. The fiducial value of the grid size ratio ∆r(i + 1)/∆r(i) is 1.02 so that the smallest cell size is 0.05, where i stands for the grid index.
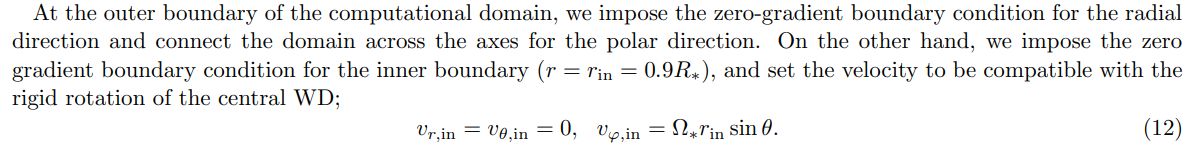
In this paper, we consider the cases with Ω∗ = [0.05, 0.07, 0.12, 0.16, 0.23, 0.35, 0.46] s−1, which correpsonds to ∼ 5-50 % of the mass shedding limit. In terms of the inner ghost cell’s density and pressure, we carefully prescribe their values to achieve a specific thermally-driven wind mass loss rate (see Sec. 2.2). Initially, we distribute a cold and homogeneous gas throughout the entire computational domain and inject the thermally-driven wind from the designated launching region. As the thermally-driven outflow reaches the outer boundary, we initiate an aligned dipole field at the inner boundary, facilitating the transformation of the wind into a rotating magnetic wind (see Sec. 2.3).
2.2. Wind launching region
We initialize our simulation with a cold, homogeneous, isotropic and non-magnetized atmosphere, and set up a “wind launching region” [2] with a width of D near the WD surface, where the mass is injected to the computational domain to mimic the mass loading due to the carbon burning around the surface of massive WD merger product. To do that, we implement an isotropic relaxation function for both matter and energy source terms to update density and pressure in wind launching region:
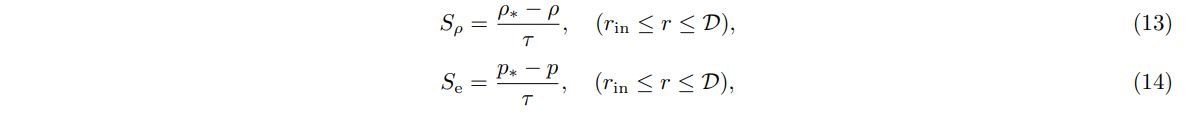
where ρ∗ and p∗ correspond to the density and pressure at the outer edge of the wind launching region. The actual value of the relaxation timescale τ is chosen to satisfy the condition,

2.3. Rotating magnetic wind

The launched gas will then corotate with the rotating magnetic field, and the magnetic torque, which depends on the resultant magnetospheric structure and the polar angle, can also contribute to the wind acceleration in addition to the thermal pressure gradient. As a result, we expect a rotating magnetic wind to start blowing in an angle dependent manner, and relax to a quasi-steady state when it reaches to the outer boundary. We simulate the rotating magnetic wind for a few 10 × the spin period after turning on the magnetic field.
[2] Note that this is originally called damping layer in the context of accreting stellar system (see Takasao et al. 2019)

