Identifying Axion Conversion in Compact Star Magnetospheres With Radio-Wave Polarization Signatures

Content Overview

Abstract and Introduction

Methods

Results

Discussions and Conclusions

Acknowledgments

Appendix A: Dielectric tensor

Appendix B: Axion electrodynamics

Appendix C: Propagation of polarized radio waves

Appendix D: Convergence and robustness tests

References

Abstract

I. INTRODUCTION

Since the 1970s, the Standard Model of particle physics has been the most successful description of all fundamental interactions other than gravity. It is a quantum field theory that has in many cases been verified experimentally mainly with accelerators. Despite the successes, the Standard Model has some theoretical shortcomings. One of these issues is the strong CP problem. The strong CP problem is a puzzle that the observations (e.g., the vanishing small electric dipole moment for neutrons) indicate a conserved CP in spite of the fact that the theory needs fine-tuning to meet such a symmetry.

Dark matter constitutes the vast majority (∼ 30%) of matter in our Universe. The evidence for the existence of dark matter has been abundant and convincing over the past several decades (e.g., [1–4]). Nevertheless, it seems that no particles within the Standard Model can play the role required of being cold, stable, and weakly coupled.

At present, a large number of terrestrial experiments have been made to probe the parameter space of axion-photon couplings. The axion haloscopes have been designed to search for photon signals from axions using the microwave cavity resonators. Experiments based on such ideas include examples of the Rochester–Brookhaven–Fermilab [10], University of Florida [11] and ADMX [12–15].

Despite those terrestrial experiments, a variety of astrophysical and cosmological observations can also be used to constrain the parameter space of axions or axionlike particles. The ratio of horizontal branch stars to red giants in the Galactic globular clusters is affected by axion-photon conversion inside stars and can be used to place a constraint on axion-photon couplings [16]. A cosmological example is using the x-ray emission excess from axion-photon conversion in the magnetic fields offered by the clusters of galaxies [17]

Recently, it is widely discussed that axions may convert to radio frequency photons in the magnetosphere of neutron stars, a compact star with surface strong magnetic field [18]. The radio signature of such a process is a narrow spectral line at a frequency mainly determined by the axion mass [19–22]. Reference [23] first employed the ray tracing method to obtain detailed observational properties of such process. This was further developed to account for light refraction and Doppler broadening in [24, 25]. Also, a variety of groups have begun to work on analyzing radio data to search for evidence of axion conversion [26–30].

In this work, we investigate the polarization properties of axion conversion in the magnetosphere of compact stars. Polarizations have been briefly discussed in the supplemental material of [20], where they gave an analytical description of the polarization profile by assuming radial trajectories for axions and converted photons. We extend the up-to-date ray tracing method to provide more accurate polarization properties by building a detailed numerical model for calculating axion-induced emission from compact star systems. Those unique polarization signatures can be helpful in the future to identify axion-induced radio signals (AIRSs) and mitigate potential false alarms.

The remainder of this paper is organized as follows. In Sec. II, we describe the methods for calculating axioninduced emission, paying particular attention to polarization properties. In Sec. III, we show the results of our calculation. Finally, we give a conclusion in Sec. IV.

II. METHODS

A. Axion-photon conversion

To derive the axion-photon conversion probability, we start from the standard Lagrangian for the axion, photon, and their couplings. Using the Euler-Lagrangian equation, Ohm’s law, and assuming that the dielectric tensor and magnetic field are time invariant, the equations of motion for electric field E and axion field a are (see, e.g., [20–22, 25])

B. Magnetosphere

In order to determine the plasma frequency, a detailed model describing the magnetosphere of compact stars is required. We adopt the classical Goldreich-Julian (GJ) model [32]. The GJ model assumes a static and corotating magnetosphere in the presence of a dipole magnetic field given by[1]

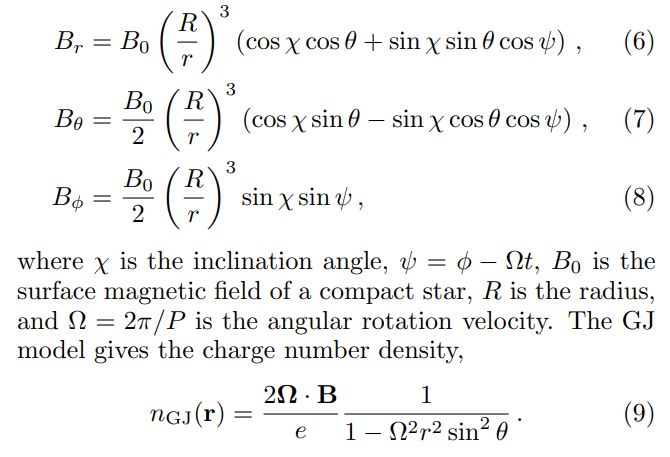
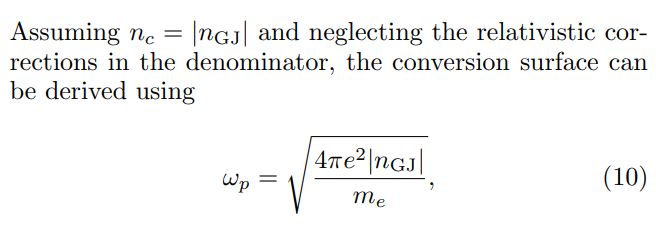
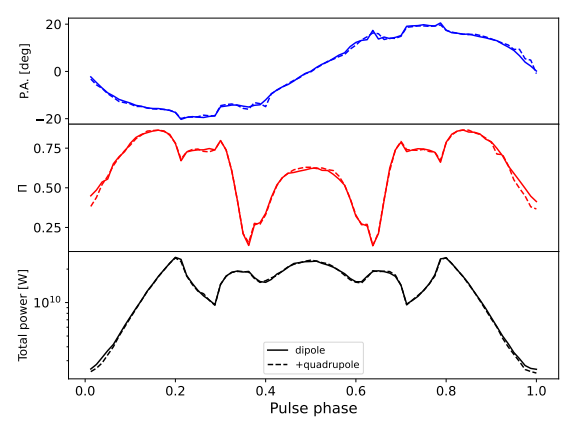
and the resonant conversion condition ωp = ma. In practice, the GJ density may not give the true charge density in the magnetosphere; that electron density can be 100– 1000 times larger [31]. In addition, dipole magnetic field configuration may not hold when approaching the surface of compact stars; it will be more appropriate to include multipolar fields [34]. Although we tested the effects of multipolar fields with a perturbation of approximately 10% quadrupole components, more rigorous work is left for future work.

C. Axion density

In this paper, as axions are regarded as the dark matter counterpart, the terms “axion” and “dark matter” are interchangeable in the following text. In general, the intensity of AIRSs equals axion flux density times axionphoton conversion probability. Thus, the distribution function is required to derive the local axion density near a compact star (CS). According to Liouville’s theorem, the distribution function is conserved along trajectories, namely,

D. Polarization

Thus, the Stokes parameters are calculated as

With the total Stokes parameters, one can derive degree of linear polarization (Π) and position angle (χ) using the definitions of

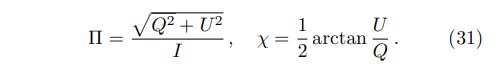
E. Ray tracing

Ray tracing is a technique of computer graphics to simulate lighting scenes. The ray tracing method obtains an image by tracing the path of the light originating from receivers toward the light sources. The basic algorithm of the ray tracing is as follows: (1) grid the image plane into small pixels; (2) determine each ray path according to the receiver position and the center of a pixel in the image plane; (3) trace each ray backward according to the geometric optics until hitting the emitter; and (4) sum the contribution of image pixels to compute the observed quantities.

This method was first introduced in Ref. [23] to obtain the observational properties of axion-induced emission. It was further developed to consider an inhomogeneous and time-dependent magnetosphere as well as including the effects of gravity in [24]. At the same time, Ref. [25] also tried to investigate the plasma effects on the converted photons’ propagation. However, Ref. [25] employed a forward ray tracing method, where photons start from the conversion point and are traced forward to the celestial sphere at infinity. The distinction between backward and forward ray tracing is only methodological and should not give a significant difference in the final results. In our framework, we use the backward ray tracing method as was used in [23, 24].

With the ray tracing method, the flux of axion-induced emission can be calculated with [23, 24]

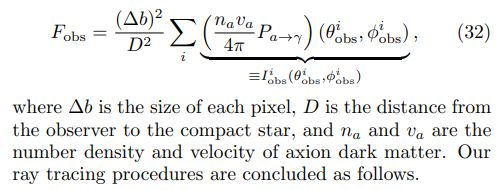
1. First, we define the projection image plane as a square plane perpendicular to the line of sight toward the compact star at a distance D from Earth. This plane is located at a distance d from the compact star. The latter distance is chosen to be larger than the maximum distance at which the resonant axion-photon conversion occurs. The total area of the projection image plane should be large enough to cover the whole conversion region. This plane is divided into square pixels of size ∆b, whose center identifies a specific photon trajectory i.

2. For each pixel, we simulate photon trajectory toward a compact star by numerically computing its geodesic starting from the center of the corresponding pixel. The direction of initial velocity is taken to be perpendicular to the projection plane.

5. The total axion-induced emission power is obtained by summing over all pixels in the projection image plane. The total Stokes parameters are calculated in the same way as is shown in Eqs. (27)–(30).

We consider two photon propagation models in this paper, propagation in vacuum [23] and in cold plasma [24]. We start with deriving the covariant theory of photon propagation using the eikonal equation [37], where the eikonal can be written as

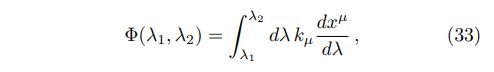
using calculus of variation and one obtains

Including plasma refraction and curved spacetime has two accompanying effects: plasma lensing and gravitational redshift. They can be concluded in (see [24])

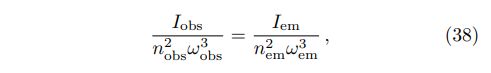
where subscripts “obs” and “em” represent quantities obtained at the location of the projection image plane and the conversion region, respectively. Taking a Schwarzschild metric for the compact star gives gravitational redshift as

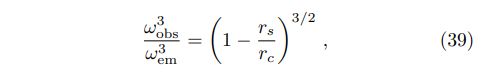
Furthermore, the influence on polarization due to light bending should be studied carefully. For curved photon trajectories, the directions of 3-momentum for different photons are different at the location of conversion points. Therefore, the basis vectors defined in Eq. (19) are not the same for different photons, and then Stokes parameters cannot be added directly using Eqs. (27)–(30). Instead, we utilize the following equation to parallel transport the polarization vectors [40]:

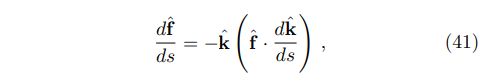
where kˆ is the unit vector for the propagation direction, s is the distance along the light ray, and ˆf is the unit polarization vector. This propagation law can be derived from Maxwell’s equations using eikonal approximation and is shown to be consistent with Fermi-Walker transport in three-dimensional space. Also, if we regard the refractive index as a space metric, this formula implies that the unit polarization vector is parallel transported along the light ray (see Appendix C). With this formula, unit polarization vectors can be transported to the projection image plane where the basis vectors are the same, whereupon we can add them incoherently as described in the ray tracing procedure.

III. RESULTS

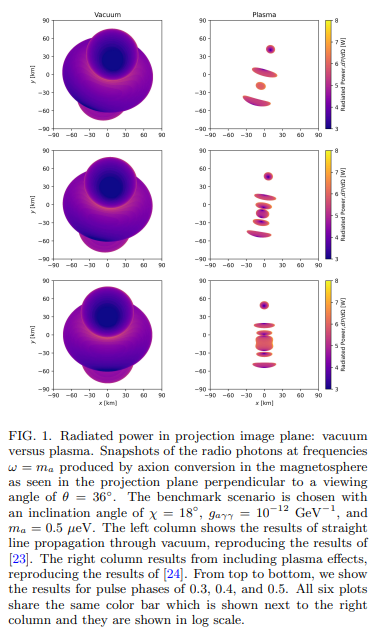
A. Projection image

B. Axion-induced emission pulse profile

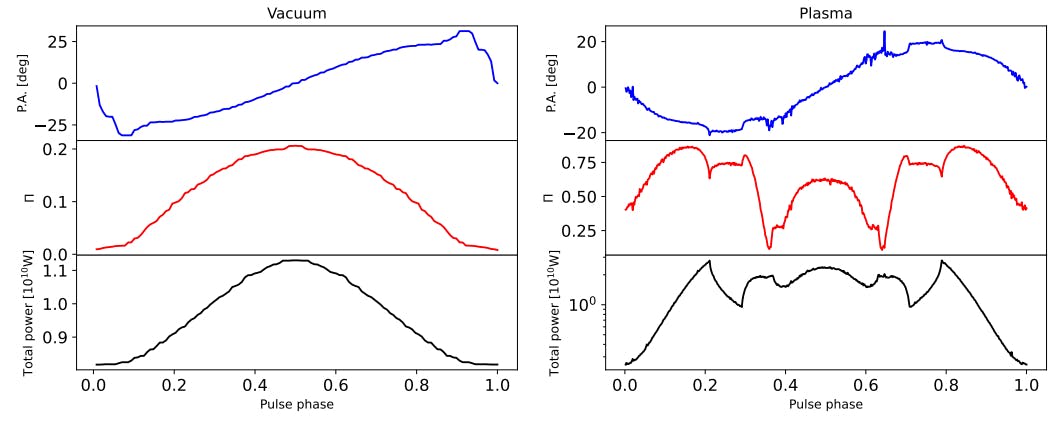
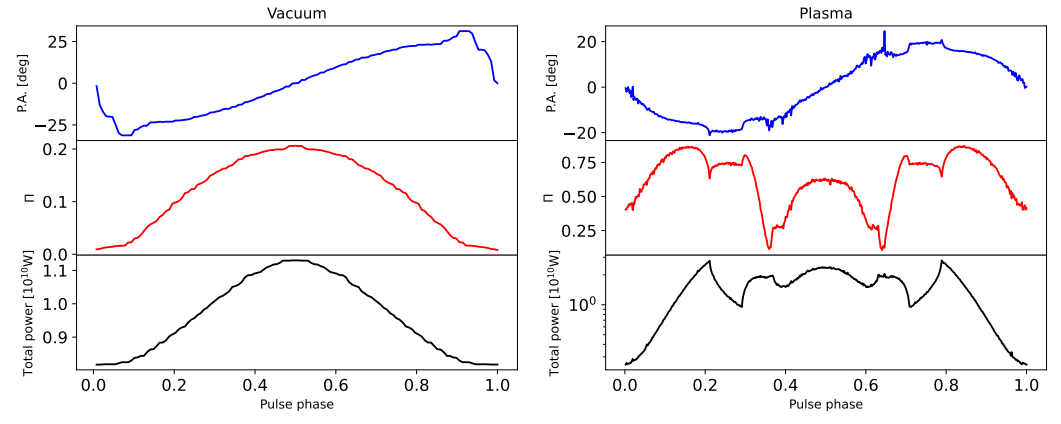
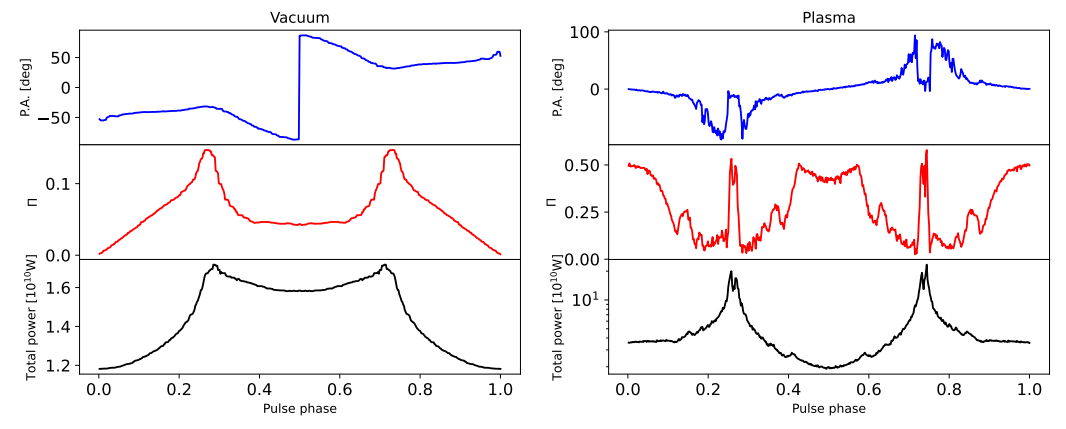
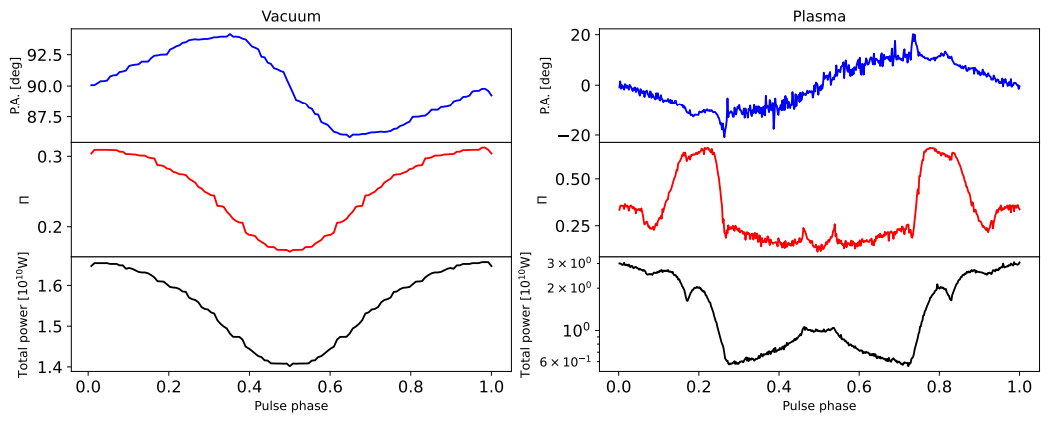
ion power (assuming the contribution of all the pixels) along with polarization properties as a function of pulsar rotational phases. The same as the projection image, we show the results of both the vacuum case and plasma case for comparison. The three figures correspond to three different viewing angles θ = 36◦ , 54◦ , and 72◦ , while inclination angle, axion mass, and axion-photon coupling constants are the same as before. Within each figure, the upper panel is the position angle of polarization, the middle panel is the degree of linear polarization, and the lower one is axion-induced emission pulse profile in units of watts.

From the three lower panels, as mentioned above, including plasma effects does not decrease the maximum radiated power significantly. However, the profile shape changed significantly so that the contrast (i.e., the pulse amplitude divided by mean flux) of the signal pulse becomes higher. It also causes larger variations concerning different viewing angles. From the three middle panels, a larger variation also occurs in polarizations. First, we find that the degree of linear polarization changes along with axion-induced emission power for the vacuum case, while it does not evolve along with total power in the plasma case and gets more complicated. Second, the degree of linear polarization in the vacuum case ranges from 0 to 0.2 (θ = 36◦ ), while it gets higher in the plasma case, ranging from 0.1 to 0.8 (θ = 36◦ ). This can be explained qualitatively. In our framework of calculating polarizations, we assumed 100% linear polarization for each pixel. To obtain total polarizations, we sum over all pixels incoherently, which decreases the degree of linear polarization. However, as can be seen from Fig. 1, including plasma effects splits the projection image into several smaller regions, and within each region the degree of linear polarization is high due to the pixels therein sharing similar position angles. Thus, summing over these localized highly linearly polarized regions produces a higher degree of linear polarization.

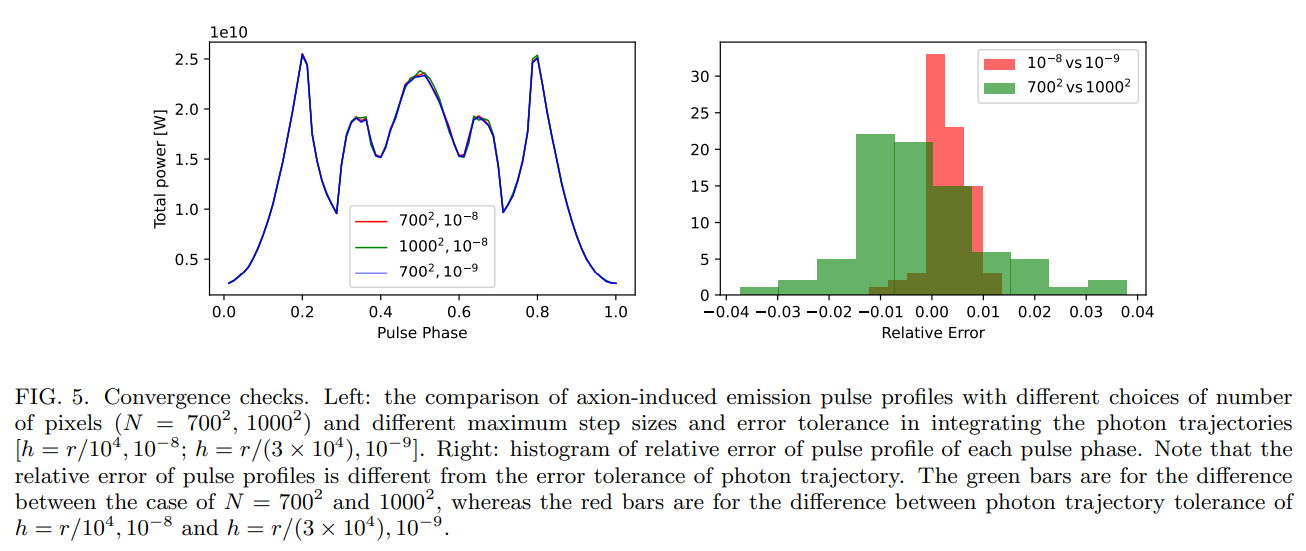
C. Convergence and robustness tests

We check the convergence and robustness of our calculation by comparing the results computed with different setups, i.e., number of pixels, integration step size, and small perturbations to magnetic field models. The results show that our calculation achieves convergence at the 7% level for different numbers of pixels and 3% level for a different choice of step size. Also, we note that a 10% perturbation to the dipole magnetic field configuration will not make a significant difference to the AIRS pulse profile or polarization. The details can be found in Appendix D.

IV. DISCUSSIONS AND CONCLUSIONS

In this paper, we have developed the framework to numerically compute the AIRSs from the magnetosphere of neutron star systems, where the intensity and polarization properties can be computed with the ray tracing method.

We find that an inclined magnetic field configuration of a neutron star leads to nontrivial polarization structures in AIRSs. Our calculation reveals that the AIRSs are dominated with linear polarization, which can be even higher considering plasma effects in photon propagation. We note that the position angle of linear polarization for the AIRSs does not follow the well-known “S” curve seen in many pulsars and modeled by the rotating vector model [43]. In our case, although the direction of the electric field of AIRSs at the emission point still follows the local magnetic field direction, the parallel transport and superposition of polarization vectors lead to a more complex situation. Thus, the AIRSs can be identified from pulsar emission (if any) by (1) a narrow band radio signal with a frequency centered at axion mass, (2) a distinct polarization feature within the narrow frequency band compared to the neighbor frequencies, and (3) linear polarization being dominant in the narrow band. Given that radio frequency interference is usually circularly polarized and pulsar radiation properties in general evolve smoothly as functions of frequency, the polarization feature will help us truly “identify” the axion events in future observations.

There are three caveats in our modeling. We excluded the region where the WKB approximation is invalid, assumed an isotropic distribution of dark matter particles, and adopted the stationary GJ magnetosphere model. As one would expect, the AIRS flux is low in the region where WKB approximation is invalid and dark matter should be isotropic at the small scale of the pulsar magnetosphere; the key issue here is the unknown magnetic field configuration. We had estimated the effects of the magnetic field configuration via tests of perturbing the dipole field. Since the dominant radiation originates from the low altitude (strong magnetic field and higher plasma density), we expect the surface magnetic field of neutron stars plays a vital role in determining the properties of AIRSs. In the future, a more realistic model on AIRSs is required to account for the effect.

At low altitudes, the axion-photon conversion probability gets higher due to the higher magnetic field Eq. (4), thus giving a peak to the pulse profile at those phases. Thus, if the viewing angle is 36◦ , then we would expect a peak at the pulse phase of 0.5 (since 36◦ = −18◦ + 54◦ ), as is shown in Fig. 3. If the viewing angle is 72◦ , then a peak should be expected at the pulse phase of 0 or 1 (since 72◦ = 18◦ + 54◦ , see Fig. 4).

ACKNOWLEDGMENTS

This work is supported by the National SKA Program of China (2020SKA0120100), the National Key R&D Program of China (2017YFA0402602), the National Nature Science Foundation Grant No. 12041303, the CASMPG LEGACY project, and funding from the MaxPlanck Partner Group.

Appendix A: Dielectric tensor

In this appendix, we describe the derivation of the cold plasma dielectric tensor relevant for solving axion electrodynamics in Sec. II A. We follow the single particle theory here. For the current problem, the single particle theory delivers the same results as the more refined kinetic theory for plasma [45]. The equation of motion for a nonrelativistic charged particle is

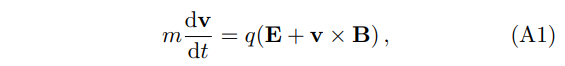
along with the expression for the current,

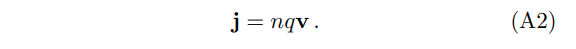
Appendix B: Axion electrodynamics

In this appendix, we revisit the derivation of axionphoton conversion probability[20–22, 25, 46], i.e., Eq. (4). The equation of motion of axion fields and electric fields is given by Eqs. (1) and (2) and is reshown here,

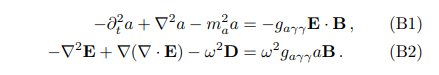
One can regard both equations as the wave equations driven by source terms on the right-hand side. We take the axion’s direction of motion to be ˆz and the direction of the magnetic field described below Eq. (A10). When considering the case of axion-photon mixing in a slowly varying and locally uniform plasma, all derivatives that do not involve the derivative in the z direction can be neglected. Therefore, with the expression of electric displacement tensor Eq. (A10), the x component of Eq. (B2) can be simplified to

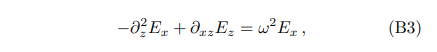
and similarly for the z component,

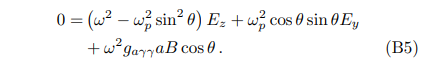
Plugging Eq. (B5) into Eq. (B4), one get

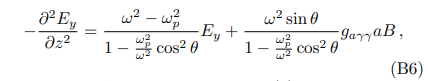
where we have defined

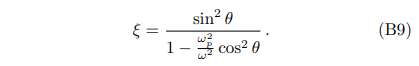
With this approximation, one can then derive the analytical expression of axion-photon conversion probability Eq. (4), which is defined as the energy flux (derived from the stress-energy tensor) ratio between the photon and axion fields [20, 23]

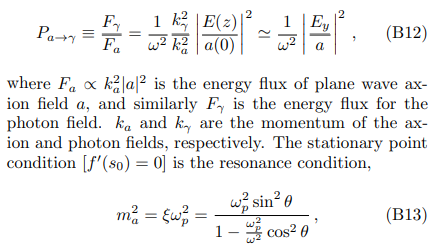
which simplifies to

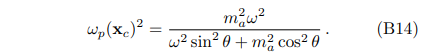
As a summary of this section, due to the WKB approximation, we regard that the axion is converted to the photon locally. The position of conversion is determined by the resonance condition, and the amplitude of the radio wave is described by the conversion probability.

Appendix C: Propagation of polarized radio waves

In this appendix, we will show that the propagation of polarized radio waves can be computed from either electrodynamics, Fermi-Walker transport (spin theory), or parallel transport (optical theory).

1. Derivation of propagation law

Starting with Maxwell’s equations,

Substitute the first equation of Eq. (C7) into the wave equation Eq. (C5) and one obtains

For isotropic media, the direction of the light ray can be taken as the direction of the averaged Poynting vector, which is

Therefore, the ray equation can be written as

The polarization base vector (ˆf) is the normalized vector of electric field amplitude that

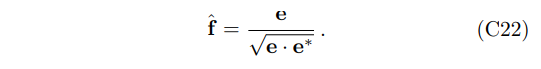
2. Derivation using Fermi-Walker transport

Therefore, Fermi-Walker transport requires that the propagation for unit polarization vector ˆf is

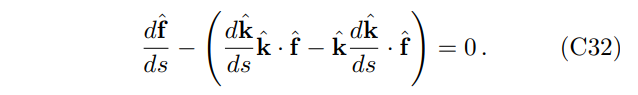
The transverse wave condition requires ˆf · kˆ = 0, and the above equation simplifies to Eq. (C29).

3. Derivation using parallel transport

Equation (41) or (C24) is equivalent to the parallel transport of the polarization vector in a curved space [47]. Because of the refractive index, the effective line element for light propagation is

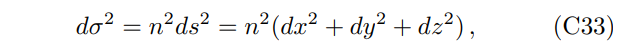
i.e., the corresponding metric is

and the connections are

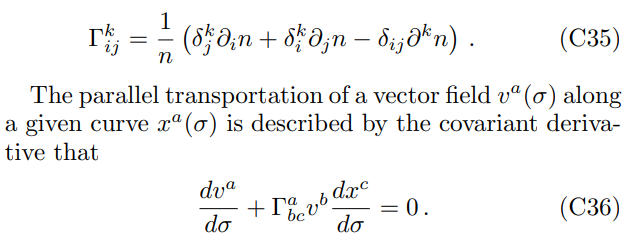
Plugging into the connection components, one obtains

which can be rewritten as

The two equations shown above can be simplified to

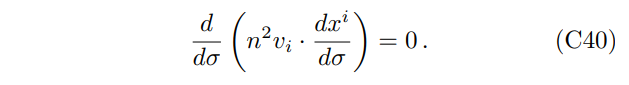
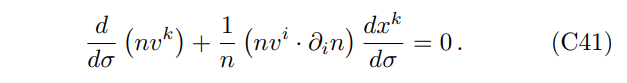
Appendix D: Convergence and robustness tests

In this appendix, we describe different convergence checks and robustness tests of our codes. These include the tests of integral and model dependence.

1. Integrals

2. Magnetic field configuration

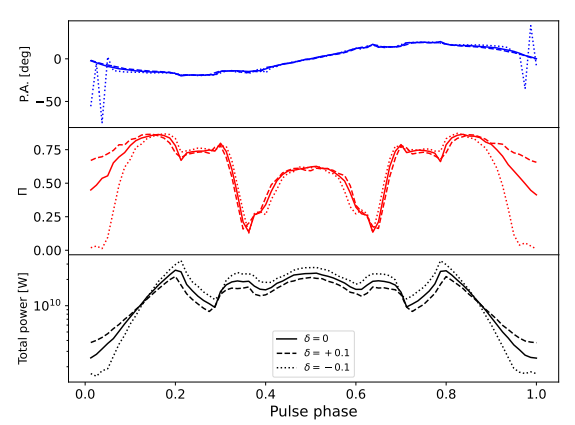
ion In the main text, we assume an exact rotating dipole field configuration for a compact star’s magnetic fields, which is unlikely in reality. So, this code test is to find out the consequence if we add a perturbation to the dipole field configuration.

First, we assume the exponent of r dependence deviates from 3; therefore, the magnetic field turns to

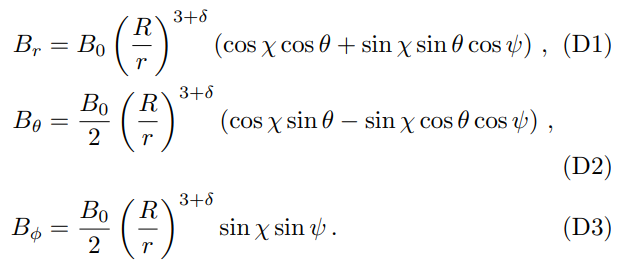
For a slight deviation, we choose δ = 0.1, −0.1, and the result is shown in Fig. 6

6. Second, we assume a perturbation to the dipole magnetic field. Then, the total magnetic field can be written as

For ϵ, we choose ϵ = 0.1, and the result of this perturbation is shown in Fig. 7.

References

[1] F. Zwicky, Die Rotverschiebung von extragalaktischen Nebeln, Helvetica Physica Acta 6, 110 (1933).

[2] V. C. Rubin and J. Ford, W. Kent, Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions, Astrophys. J. 159, 379 (1970).

[3] J. A. Tyson, G. P. Kochanski, and I. P. Dell’Antonio, Detailed Mass Map of CL 0024+1654 from Strong Lensing, ApJ 498, L107 (1998), arXiv:astro-ph/9801193 [astroph].

[4] L. Hui, Wave Dark Matter, ARA&A 59, 247 (2021), arXiv:2101.11735 [astro-ph.CO].

[5] R. D. Peccei and H. R. Quinn, CP conservation in the presence of pseudoparticles, Phys. Rev. Lett. 38, 1440 (1977).

[6] J. Preskill, M. B. Wise, and F. Wilczek, Cosmology of the invisible axion, Physics Letters B 120, 127 (1983).

[7] L. F. Abbott and P. Sikivie, A cosmological bound on the invisible axion, Physics Letters B 120, 133 (1983).

[8] M. Dine and W. Fischler, The not-so-harmless axion, Physics Letters B 120, 137 (1983).

[9] S. Weinberg, A new light boson?, Phys. Rev. Lett. 40, 223 (1978).

[10] S. DePanfilis, A. C. Melissinos, B. E. Moskowitz, J. T. Rogers, Y. K. Semertzidis, W. U. Wuensch, H. J. Halama, A. G. Prodell, W. B. Fowler, and F. A. Nezrick, Limits on the abundance and coupling of cosmic axions at 4.5 < ma < 5.0 µev, Phys. Rev. Lett. 59, 839 (1987).

[11] C. Hagmann, P. Sikivie, N. S. Sullivan, and D. B. Tanner, Results from a search for cosmic axions, Phys. Rev. D 42, 1297 (1990).

[12] S. J. Asztalos et al. (ADMX), SQUID-Based Microwave Cavity Search for Dark-Matter Axions, Phys. Rev. Lett. 104, 041301 (2010), arXiv:0910.5914 [astro-ph.CO].

[13] N. Du et al. (ADMX), Search for Invisible Axion Dark Matter with the Axion Dark Matter Experiment, Phys. Rev. Lett. 120, 151301 (2018), arXiv:1804.05750 [hepex].

[14] T. Braine et al. (ADMX), Extended Search for the Invisible Axion with the Axion Dark Matter Experiment, Phys. Rev. Lett. 124, 101303 (2020), arXiv:1910.08638 [hep-ex].

[15] C. Bartram et al. (ADMX Collaboration), Search for invisible axion dark matter in the 3.3 − −4.2 µeV mass range, Phys. Rev. Lett. 127, 261803 (2021).

[16] A. Ayala, I. Dom´ınguez, M. Giannotti, A. Mirizzi, and O. Straniero, Revisiting the Bound on Axion-Photon Coupling from Globular Clusters, Phys. Rev. Lett. 113, 191302 (2014), arXiv:1406.6053 [astro-ph.SR].

[17] J. P. Conlon and M. C. D. Marsh, Excess Astrophysical Photons from a 0.1-1 keV Cosmic Axion Background, Phys. Rev. Lett. 111, 151301 (2013), arXiv:1305.3603 [astro-ph.CO].

[18] R. N. Manchester and J. H. Taylor, Pulsars (Freeman WH, San Francisco, 1977).

[19] M. S. Pshirkov and S. B. Popov, Conversion of dark matter axions to photons in magnetospheres of neutron stars, Soviet Journal of Experimental and Theoretical Physics 108, 384 (2009), arXiv:0711.1264 [astro-ph].

[20] A. Hook, Y. Kahn, B. R. Safdi, and Z. Sun, Radio Signals from Axion Dark Matter Conversion in Neutron Star Magnetospheres, Phys. Rev. Lett. 121, 241102 (2018), arXiv:1804.03145 [hep-ph].

[21] R. A. Battye, B. Garbrecht, J. I. McDonald, F. Pace, and S. Srinivasan, Dark matter axion detection in the radio/mm waveband, Phys. Rev. D 102, 023504 (2020), arXiv:1910.11907 [astro-ph.CO].

[22] A. J. Millar, S. Baum, M. Lawson, and M. C. D. Marsh, Axion-photon conversion in strongly magnetised plasmas, J. Cosmology Astropart. Phys. 2021, 013 (2021), arXiv:2107.07399 [hep-ph].

[23] M. Leroy, M. Chianese, T. D. P. Edwards, and C. Weniger, Radio signal of axion-photon conversion in neutron stars: A ray tracing analysis, Phys. Rev. D 101, 123003 (2020), arXiv:1912.08815 [hep-ph].

[24] R. A. Battye, B. Garbrecht, J. McDonald, and S. Srinivasan, Radio line properties of axion dark matter conversion in neutron stars, Journal of High Energy Physics 2021, 105 (2021), arXiv:2104.08290 [hep-ph].

[25] S. J. Witte, D. Noordhuis, T. D. P. Edwards, and C. Weniger, Axion-photon conversion in neutron star magnetospheres: The role of the plasma in the GoldreichJulian model, Phys. Rev. D 104, 103030 (2021), arXiv:2104.07670 [hep-ph].

[26] J. Darling, Search for Axionic Dark Matter Using the Magnetar PSR J1745-2900, Phys. Rev. Lett. 125, 121103 (2020), arXiv:2008.01877 [astro-ph.CO].

[27] J. Darling, New Limits on Axionic Dark Matter from the Magnetar PSR J1745-2900, ApJ 900, L28 (2020), arXiv:2008.11188 [astro-ph.CO].

[28] J. W. Foster, Y. Kahn, O. Macias, Z. Sun, R. P. Eatough, V. I. Kondratiev, W. M. Peters, C. Weniger, and B. R. Safdi, Green Bank and Effelsberg Radio Telescope Searches for Axion Dark Matter Conversion in Neutron Star Magnetospheres, Phys. Rev. Lett. 125, 171301 (2020), arXiv:2004.00011 [astro-ph.CO].

[29] R. A. Battye, J. Darling, J. I. McDonald, and S. Srinivasan, Towards robust constraints on axion dark matter using PSR J1745-2900, Phys. Rev. D 105, L021305 (2022), arXiv:2107.01225 [astro-ph.CO].

[30] J. W. Foster, S. J. Witte, M. Lawson, T. Linden, V. Gajjar, C. Weniger, and B. R. Safdi, Extraterrestrial Axion Search with the Breakthrough Listen Galactic Center Survey, Phys. Rev. Lett. 129, 251102 (2022), arXiv:2202.08274 [astro-ph.CO].

[31] M. A. Ruderman and P. G. Sutherland, Theory of pulsars: polar gaps, sparks, and coherent microwave radiation., Astrophys. J. 196, 51 (1975).

[32] P. Goldreich and W. H. Julian, Pulsar Electrodynamics, Astrophys. J. 157, 869 (1969).

[33] F. C. Michel, Theory of pulsar magnetospheres, Reviews of Modern Physics 54, 1 (1982).

[34] J. A. Gil, G. I. Melikidze, and D. Mitra, Modelling of the surface magnetic field in neutron stars: Application to radio pulsars, A&A 388, 235 (2002), arXiv:astroph/0111474 [astro-ph].

[35] M. S. Alenazi and P. Gondolo, Phase-space distribution of unbound dark matter near the Sun, Phys. Rev. D 74, 083518 (2006), arXiv:astro-ph/0608390 [astro-ph].

[36] G. B. Rybicki and A. P. Lightman, Radiative processes in astrophysics (Wiley-Interscience, New York, 1979).

[37] S. Weinberg, Eikonal Method in Magnetohydrodynamics, Physical Review 126, 1899 (1962).

[38] D. Melrose, Quantum Plasmadynamics: Unmagnetized Plasmas, 1st ed. (Springer Publishing Company, Incorporated, 2007).

[39] M. Born and E. Wolf, Principles of Optics (Cambridge University Press, 1999).

[40] K. S. Thorne and R. D. Blandford, Modern Classical Physics: Optics, Fluids, Plasmas, Elasticity, Relativity, and Statistical Physics (Princeton University Press, 2017).

[41] E. Fehlberg, Classical fourth-and lower order runge-kutta formulas with stepsize control and their application to heat transfer problems, Computing 6, 61 (1970).

[42] D. L. Kaplan and M. H. van Kerkwijk, Constraining the Spin-down of the Nearby Isolated Neutron Star RX J0806.4-4123, and Implications for the Population of Nearby Neutron Stars, Astrophys. J. 705, 798 (2009), arXiv:0909.5218 [astro-ph.HE].

[43] V. Radhakrishnan and D. J. Cooke, Magnetic Poles and the Polarization Structure of Pulsar Radiation, Astrophys. Lett. 3, 225 (1969).

[44] R. A. Battye, M. J. Keith, J. I. McDonald, S. Srinivasan, B. W. Stappers, and P. Weltevrede, Searching for Time-Dependent Axion Dark Matter Signals in Pulsars, arXiv e-prints , arXiv:2303.11792 (2023), arXiv:2303.11792 [astro-ph.CO].

[45] D. G. Swanson, Plasma waves (Academic Press, New York, 1989).

[46] G. Raffelt and L. Stodolsky, Mixing of the photon with low-mass particles, Phys. Rev. D 37, 1237 (1988).

[47] R. K. Luneburg, Mathematical Theory of Optics (University of California Press, 1964).

[1] Strictly speaking, the GJ model is not applicable to inclined rotator nor active pulsars [33]. However, since we are mainly interested in the region close to the star surface, the GJ model provides a reasonable start.

[2] Note that this is valid as long as the projection image plane is placed at a relatively large distance.